Priceless
[VSLAM] 동차좌표계(Homogeneous Coordinates) 본문
Projective Geometry
사영기하학
3D world vs Photo
3차원 세상은 무한의 개념을 숫자로 표현할 수 없다
기차길이 평행하다 하더라도
기차길 위에서 사진을 찍으면 멀어지면서 사라지는 곳에서 교차한다(vanishing point)
원근법
3차원 공간을 2차원에 투영하면서 깊이 정보가 소실된다(depth)
차원 변환 과정에서 3차원에서의 평행 조건과 수직 조건이 2차원의 투영 결과에서 사라진다(parallelism & orthogonality)
또한 범위와 단위도 사라진다(scale)
다만 직선이 그대로 직선으로 나오는 점은 동일하다
Vanishing Point
3차원의 평행선의 끝을 알 수 없지만
2차원에 투영하는 경우 끝 점을 관측할 수 있다
이 점을 vanishing point라고 한다
3차원의 무한한 공간을 2차원의 특정 공간에 매핑할 수 있다
Hierachies of geometries
- Euclidean transformation: rotation과 translation을 표현할 수 있다
- Similarity transformation: Euclidean transformation에서 모든 방향으로 scale이 동일하게 변화하는 uniform scaling을 표현할 수 있지만
length 정보가 사라진다
- Affine transformation: Similarity transformation에서 방향에 따라서 달라지는 scaling인 non-uniform scaling과 shear(전단력)를 표현할 수 있지만
angle, length-ratio 정보가 사라진다
- Projective transformation: Affine transformation에서 무한대의 거리에 있는 점에 대해 원근법을 통해 차원 축소를 하는 projection을 표현할 수 있지만
incidence(투사각, 투영각)과 cross-ratio(비조화비, 같은 직선 위에 있는 네 점의 유일한 사영 불변량) 정보가 사라진다

Homogeneous Coordinates
동차좌표계
projective coordinates와 비교
projective coordinate 는 n+1차원을 n차원으로 투영한다면
homogeneous coordinates는 x,y,z와 scale 정보를 가지고 3차원 -> 2차원 뿐만 아니라 고차원으로도 투영 가능하다

정의
특정 객체에 0이 아닌 다른 수를 곱해도 두 객체는 같은 객체를 의미한다
기존의 euclidean coordinates와 다른 점이다

이를 표시하기 위해 scale 성분을 추가로 작성한다
euclidean space에서는 scale을 포함하지 않지만 (cartesian coordinates)
projective space에서는 아래에 scale을 포함한다 (homogeneous coordinates)

Projective space -visualized
scale space
왼쪽 이미지는 2D projective space를 나타낸다
u, v 축은 기존의 x, y 축을 의미한다
w는 homogeneous coordinates에서 scale을 나타낸다
scale이 1인 공간을 나타내는 평면이다
euclidean space는 projective space의 하위 개념이다
scale이 1인 특별한 케이스이다
euclidean space에서 0차원인 정보가
projective space에서는 1차원으로 표현된다
projective space에서는 사영된 공간에 비해 항상 한 차원이 추가된다
추가되는 차원은 선으로 표현된다
선에 있는 모든 데이터는 같은 정보를 나타낸다
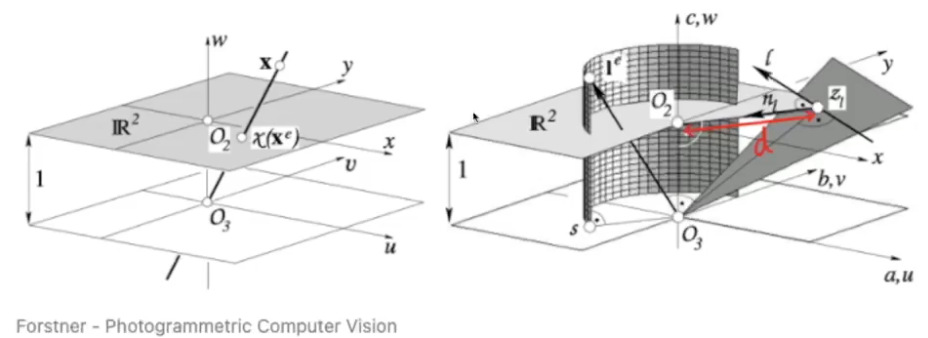
2D euclidean space에 line을 그린 경우
오른쪽 사진처럼
projective space 에서는 2차원의 정보로 표현된다
line에 대한 plane이 생긴다
Euclidean space vs Projective space
- Euclidean space
Cartesian coordinate을 사용한다
scale이 1인 projective space로, 하위 집합이다
cartesian coordinate로 표현할 경우 scale 정보를 같이 표기한다
- Projective space
Homogeneous coordinate를 사용한다
cartesian coordinate로 표현할 경우 scale을 성분에 모두 나눈 후 scale을 별도로 추가한다

SO(3) & SE(3)
Homogeneous coordinate를 행렬로 표현하는 방법
3x3 행렬의 회전인 경우
scale 정보를 (4,4) 자리에 표기한다
이동인 경우에도 마지막 자리에 추가한다

'SLAM > Visual SLAM' 카테고리의 다른 글
| [VSLAM]RANSAC (1) | 2023.11.28 |
|---|---|
| [VSLAM]Epipolar Geometry (1) | 2023.11.27 |
| [VSLAM]특징점 기술의 역사 (1) | 2023.11.25 |
| [VSLAM]카메라 센서의 구조 (0) | 2023.11.24 |
| [VSLAM]핀홀카메라 투영 (1) | 2023.11.23 |




