Priceless
[VSLAM]Triangulation 본문
General Triangulation
Motivation
개요
VSLAM을 통해 map 생성과 localization을 동시에 할 수 있는데
F 행렬과 E 행렬을 통해 두 이미지 간의 상대적인 이동치를 추정할 수 있다
위치 추정을 할 수 있다
3D 구조로 복원하기 위해서는 Triangulation이 필요하다
두 이미지 간의 상대적인 회전 값을 알고 feature 간의 correspondence를 알고 있을 때
실제 point가 있는 위치의 x,y,z 좌표 값을 알 수 있다
이를 통해 2d 에서 3d 로 매핑이 가능하다
서로 매치된 feature에서 나온 ray를 연결하면 하나의 3d 포인트에서 만난다
triangulation을 통해 두 쌍의 correspondence를 구해 두 개의 3d point를 구했고 두 점 간의 거리도 알 수 있다

Geometric solution
수학적 정의
두 개의 카메라 P, Q와 카메라에서 나오는 ray인 lambda 와 mu가 있다
이론적으로 두 ray가 한 3D point에서 만나야 한다

하지만 현실적으로 feature keypoint에 노이즈가 있으므로
두 ray가 3D 공간에서 한 점에서 만나지 않고 조금 떨어지게 된다
이를 해결하기 위해 두 ray가 가장 가까이 만나는 곳의 가운데 점으로 설정한다
이 경우 두 feature 포인트에 같은 노이즈가 있다고 간주하고
두 ray를 조금씩 옮겨 3D point를 찾는다

이를 위한 두 ray를 표현하는 식이 필요하다
r 과 s 는 ray를 표현하는 방향 벡터, 거리값을 표현하는 lambda와 mu, 시작 위치를 나타내는 p와 q다
f와 g에 해당하는 위치를 찾기 위해 값을 넣는다
r과 s를 구하기 위해 x의 프라임 값들을 구한다


Orthogonal projection
하지만 이 두 수식으로 intersection을 구할 수 없다

교점인 h를 구하기 위해서 수직하는 벡터의 내적은 0인 것을 활용한다
f와 g를 대입한 후 식을 푼다
두 개의 식에 두 개의 미지수가 나타난다

위 식을 정리한다
Xo'은 왼쪽 카메라 프레임의 센터, Xo''은 오른쪽 카메라 프레임의 센터를 의미한다
이후 하나의 행렬로 정리하면 아래와 같다
크게 보면 Ax = B 형식의 행렬 등식이 나타난다
x를 구하기 위해서 양 쪽의 식 앞에 A의 역행렬을 곱한다

미지수를 풀어 lambda 와 mu를 구한다
이를 통해 F와 G를 구해 H를 알 수 있다
H에 대한 영향도가 F와 G 모두 0.5 일 때 아래와 같은 식으로 나타낼 수 있다
P와 Q의 불확실성에 따라 F와 G의 영향도가 달라지므로
H를 구하는 식이 달라질 수 있다

Stereo Triangulation
전방에 바라보는 카메라가 두 대 있는 상황의 삼각법이다
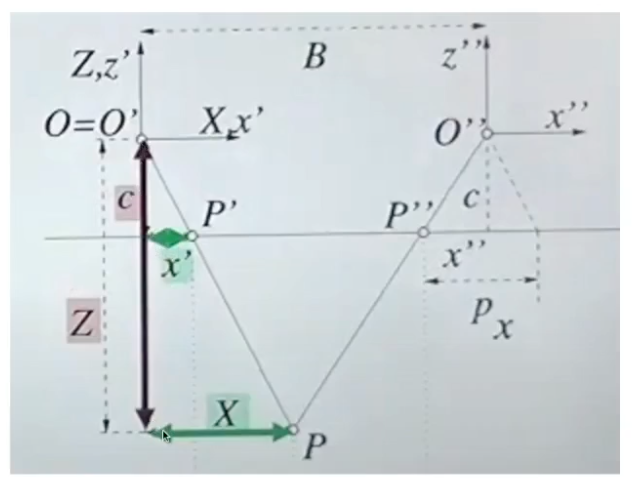
Stereo normal case
시각화
두 카메라가 전방을 바라보고 같은 plane에 있는 상황이다
두 카메라 사이의 baseline을 알고 있으며,
두 카메라에 상이 맺히는 지점인 x'과 x''을 알고 있는 상황이다
그리고 두 이미지에 나타난 feature 위치의 차이(parallax/disparity)를 알고 있다

Two view projection
두 카메라의 top view 시점에서 바라본다
두 카메라 point를 하나로 맞춰본다

닮은 꼴을 통해 z를 구하기 위해
baseline의 길이와 feature 포인트 와의 거리를 나눈다
빨간선에 나타난 닮은 꼴을 사용한다
c를 양 변에 곱해 상수 c에 비례하는 것을 알 수 있다

X에 대해서도 Z를 응용하여 구할 수 있다

Y도 똑같은 방법으로 구할 수 있지만
현실적으로 맞아 떨어질 가능성이 거의 없다
이를 보완하기 위해 두 값의 중간값으로 설정한다


'SLAM > Visual SLAM' 카테고리의 다른 글
| [VSLAM]최소자승법 (2) | 2023.12.03 |
|---|---|
| [VSLAM]Perspective N Points (2) | 2023.12.03 |
| [VSLAM]RANSAC (1) | 2023.11.28 |
| [VSLAM]Epipolar Geometry (1) | 2023.11.27 |
| [VSLAM]특징점 기술의 역사 (1) | 2023.11.25 |




