Priceless
[VSLAM]Perspective N Points 본문
Perspective N Points
PnP Problem
정의
n개의 데이터에서
2D 데이터와 3D 데이터 간의 correspondence가 주어졌을 때
world-to-camera transformation을 추론하는 문제이다
카메라가 3D 맵을 바라볼 때 correspondence를 구했다면
이 정보를 가지고 현재 카메라 pose를 추정한다
이 중 몇 개의 correspondence를 사용하냐에 따라
n의 수가 달라진다
이미지로부터 feature를 뽑고 map과 매칭하면서
map에 대해서 나의 위치를 찾을 수 있다
Localization과 관련있다
pnp는
3D point x가 담고 있는 descriptor들과 현재 뷰에서 보이는 descriptor들을 매치해서
2D to 3D correspondence를 구한다
충분한 페어의 수가 correspondence가 만들어진다면
이 데이터를 통해 카메라의 pose를 구한다
카메라의 Pose를 구하므로 6 자유도를 가지고 있다
x,y,z의 translation과 rotation을 가진다
6개의 자유도를 구하기 위해 6개의 방정식이 필요하다
2D to correspondence에서 이미지 feature인 u와 이에 해당하는 3D point P인 (u,P) 가 3쌍 필요하다
p3p 알고리즘은 noise를 전혀 고려하지 않으므로
RANSAC과 같은 rejection 알고리즘이 필요하다

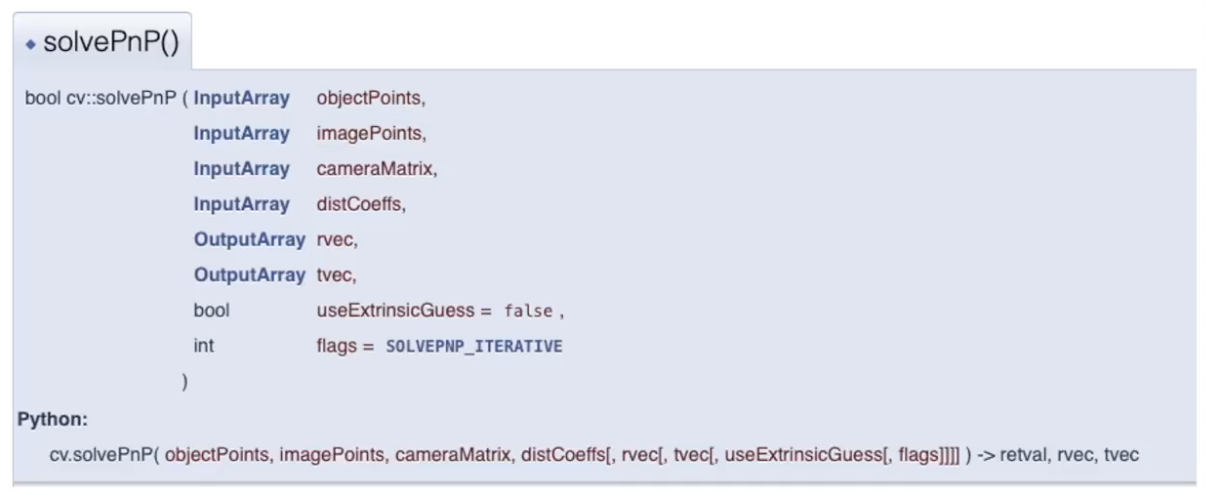
OpenCV implementation
PnP의 경우
OpenCV에 잘 구현이 되어 있다
함수의 방식을 고르기 위해 flag에 다른 값들을 입력하여
다양한 PnP 방법을 시도할 수 있다
Minimal Solver - P3P Grunert Method
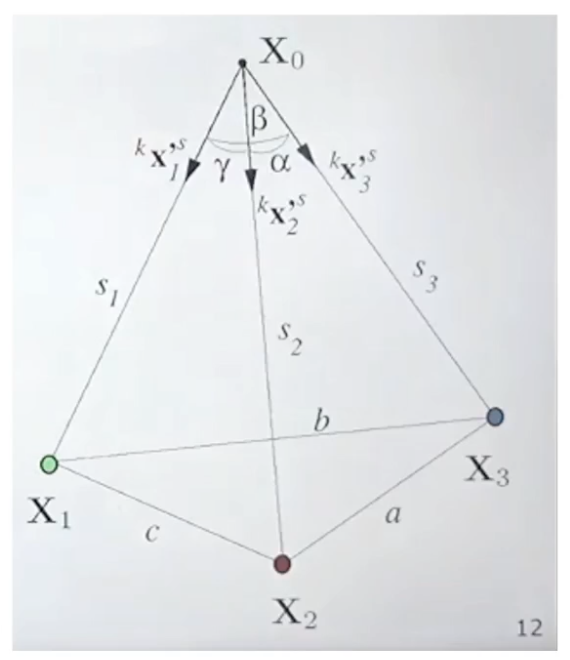
P3P
world coordinate 기준으로 세 점인 X1~3의 위치를 알고 있고
camera image의 위치로 X'1~3를 알고 있을 때
optical center로 부터 픽셀 위치를 알고 있으므로 ray들 마다의 각도를 계산할 수 있고
X1~3 까지의 거리는 알지 못하므로 ray의 길이는 알 수 없다
2-Step process
1. projection rays에 대한 길이를 추론하고
2. 길이와 ray들의 각도를 사용하여 orientation을 추론한다
표현하고 싶은 정보 X1~3는 아래와 같이 나타낼 수 있다
s는 ray의 길이, i는 인덱스, kXsi는 ray의 방향 벡터, R은 world to camera coordinate transformation의 회전 값
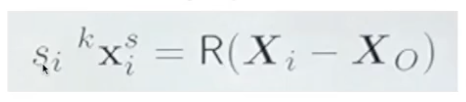
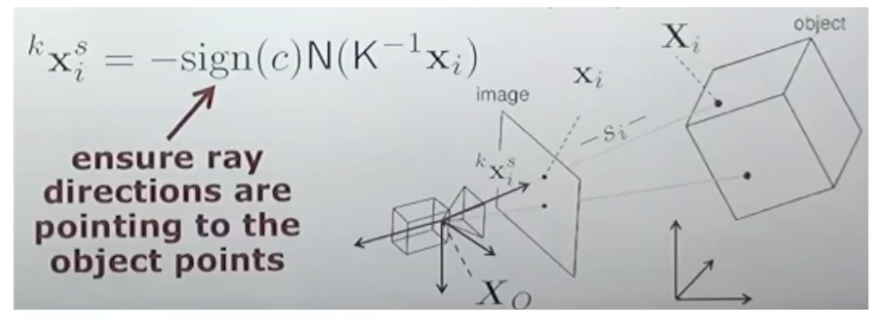
-sign(x)는 카메라 상수(focal length)를 뜻한다
보통 카메라로 들어가는 방식으로 표현하여 음수로 설정한다
N은 정면으로 가는 벡터에 법선 벡터를 의미한다
x는 방향 벡터로 사용하기 위해 거리 값을 제외한 단위 벡터로 설정한다
K의 역행렬을 구하면 다시 원래 이미지로 돌릴 수 있다
Step 1 - Get length of projection rays
ray의 길이를 구하기 위해
X1~3를 camera center에 연결한다
길이 s1~3를 설정한다
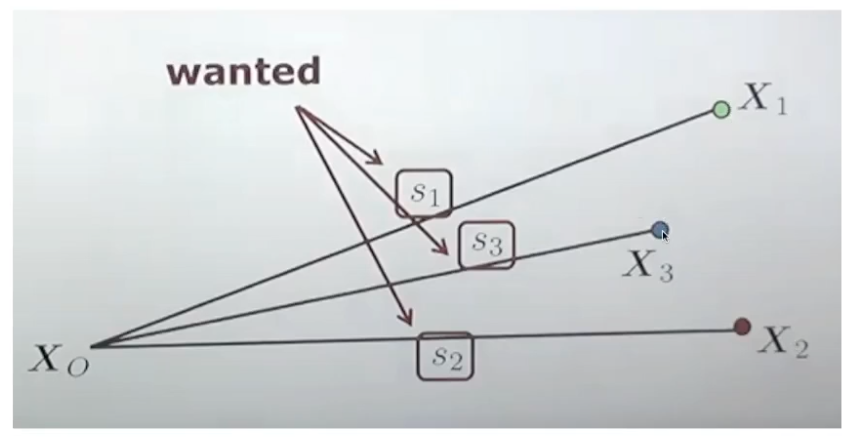
우선 ray들 간의 각도를 구한다
line 벡터를 통해 cos으로 구할 수 있다
점이 3개인 경우 모두 적용한다
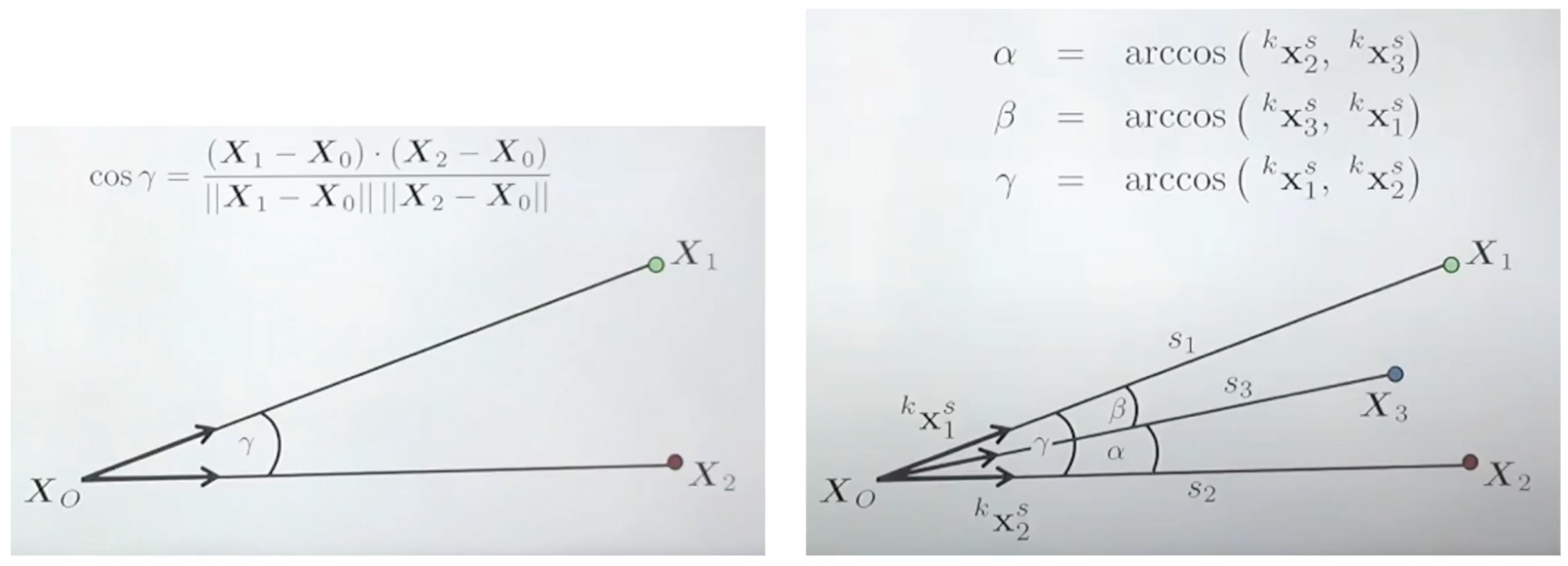
X1~3의 3D point를 알고 있으므로
3D point 간의 거리를 구할 수 있다
거리값 a~c를 구한다
이 값을 제곱하여 cosine 룰을 적용한다
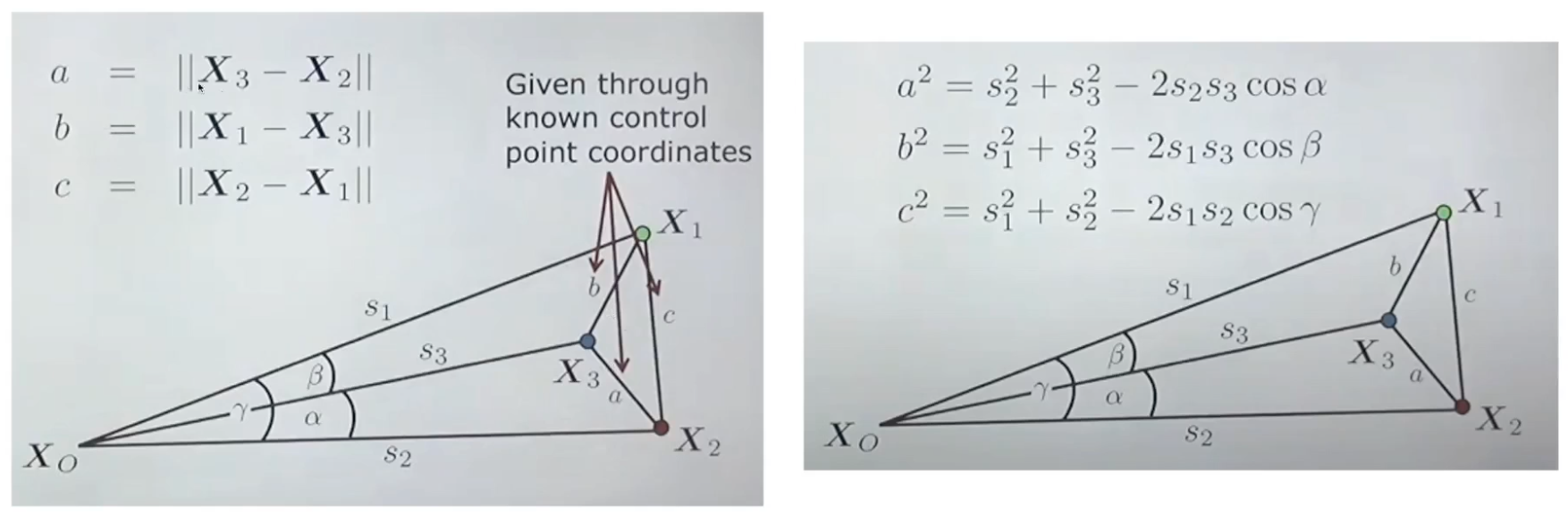
이 정보를 기반으로 거리 값을 구한다
s를 활용하여 u, v 변수를 새로 만들어 식에서 s를 대체한다
s를 치환하여 a,b,c에 대한 오른쪽과 같은 식을 구한다
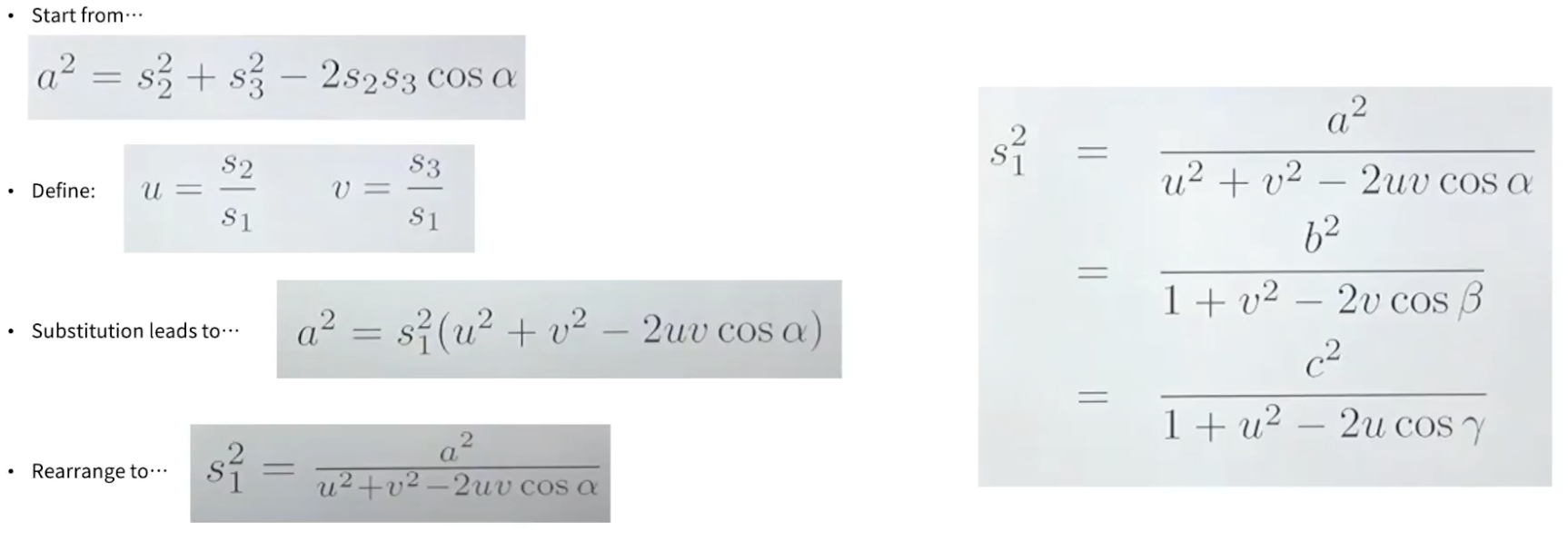
u를 식에서 없애면 아래와 같은 식이 나타난다
v만 남기면 4차 방정식이 나타난다

A 계수는 매우 복잡하게 나타난다
증명하기 보다는 코딩을 통해 바로 사용한다

V를 중심으로 풀고 나면
4차 방정식으로 풀었기 때문에
해는 4개가 나온다
4가지 중에 하나만 물리적인 실제 값이므로
나머지 3개는 실제로 존재하지 않고 기하학적으로만 존재하는 값이다
이 중 실제 물리 값을 찾기 위해
첫 번째로 다른 센서를 통해 검증을 거칠 수 있다
하지만 카메라 외의 다른 센서가 필요하다
두 번째로
다른 correspondence를 사용하여 orientation을 검증한다
이 방법을 사용하면 정확한 방법으로 구할 수 있으나
새로운 corresponse를 알아야 하므로 새로운 point를 알아야 한다
'SLAM > Visual SLAM' 카테고리의 다른 글
| [VSLAM]Bundle Adjustment (1) | 2023.12.09 |
|---|---|
| [VSLAM]최소자승법 (2) | 2023.12.03 |
| [VSLAM]Triangulation (1) | 2023.12.02 |
| [VSLAM]RANSAC (1) | 2023.11.28 |
| [VSLAM]Epipolar Geometry (1) | 2023.11.27 |




