Priceless
[VSLAM]Bundle Adjustment 본문
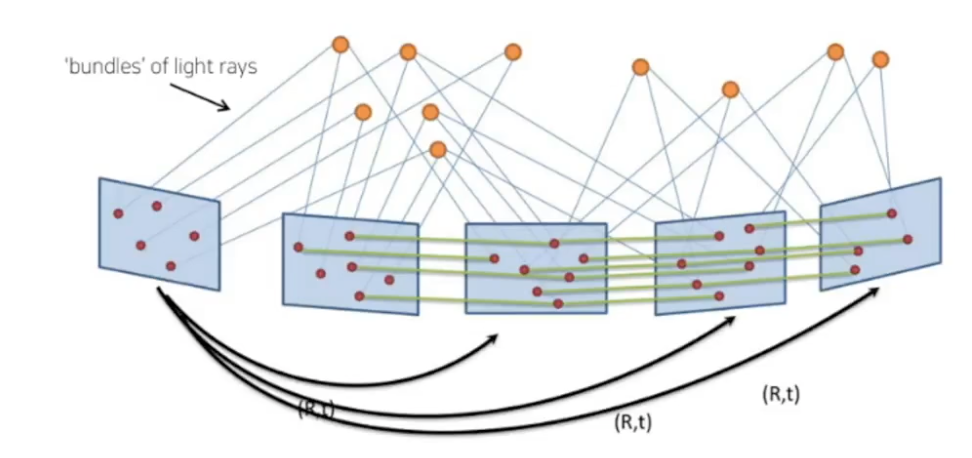
Bundle Adjustment(BA)
N-view geometry
There are N frames
Triangulation에서 수행했던 2 view geometry가 아닌
n개의 이미지를 사용한 N view image이다
여러 개의 frame이 있고 각 프레임마다 relative motion(rotation and translation)을 가지고 있다
frame마다 correspondence를 가지고 있으며, Landmark의 3D 위치도 알고 있으며,
하나의 landmark에는 두 개 이상의 2D to 3D correspondence를 가지고 있다
로봇이 이동하면서 frame마다의 motion과 observation에서 발생하는 noise가 쌓여 나타난 uncertainty를 해결하기 위해
batch SLAM 기법을 적용한다
2D-2D, 2D-3D correspondence, relative motion 등을 이용하여
카메라 pose와 3D landmark 위치를 고정하는 것이 BA의 목적이다
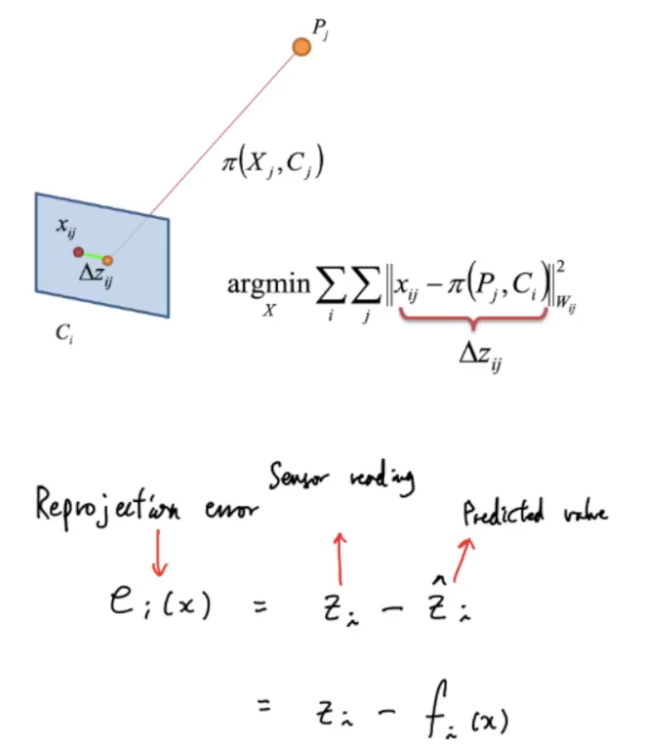
Cost function
보정은 그래프 최적화를 통해 불확실성을 해소해주는 것이다
Reprojection error
예측한 3D 랜드마크 위치가 완벽하게 정확하고 카메라의 pose 도 완벽하게 정확하면
3D 랜드마크를 image plane 에 투영했을 때
정확한 feature가 뽑힌 keypoint 위치로 투영 된다
하지만 모든 센서는 노이즈가 있고 모델링은 완벽하지 않으므로
투영하는 과정에서 나타나는 오차를 Reprojection error이라 한다
camera pose에 대한 E와 observation model 에 대한 E도
reprojection error이다
오차를 줄이기 위해
카메라의 위치를 옮기거나 예측된 Landmark의 위치를 옮겨야 한다
Nonlinear optimization
이미지 수집 과정이 linear하지 않기 때문에
최적화를 사용할 때 단순 미분이 아닌 다른 방식으로 접근해야 한다
비선형 최적화는
non-linear error parameter space(error manifold) 에서 선형 공간으로 근사시켜
최적의 값으로 이동하는 기법이다
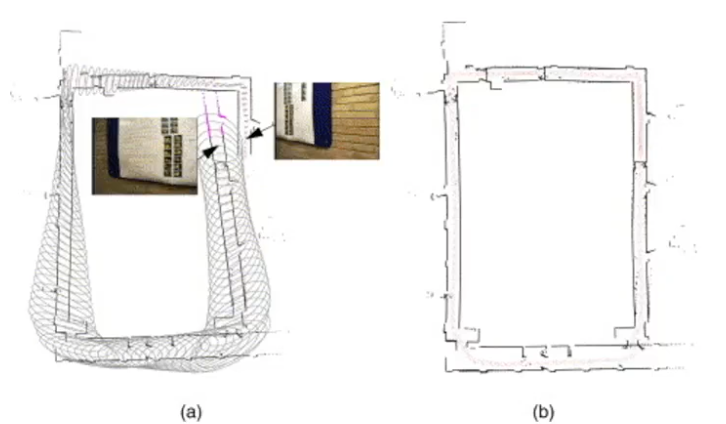
SLAM에서 Bundle Adjustment를 사용할 때
Loop closure
factor graph에서 loop가 발생할 때
해당 loop에서 누적된 motion error 과 observation error 를 BA를 통해 해소할 수 있다
Sliding-window optimization
가장 최근의 n 개의 keyframe을 가지고 BA를 수행하여
그래프 최적화를 통해 실시간으로 최적의 pose를 구한다
Nonlinear Optimization
Gauss-Newton Method
Derivation
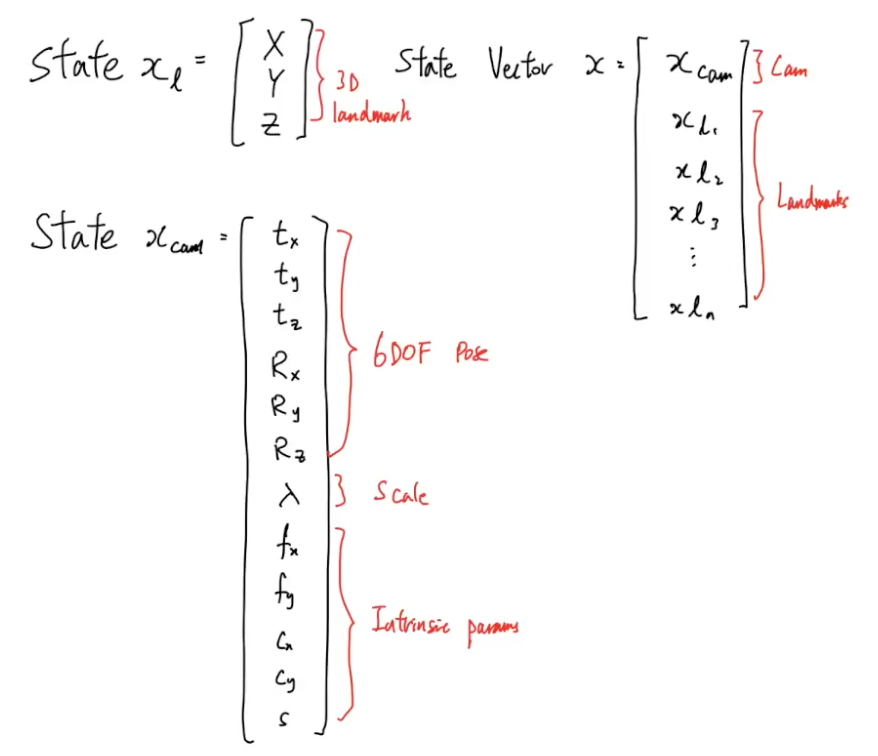
BA를 푸는데 필요한 state들은 다음으로
BA에서 사용하는 observation 식은 다음과 같다
projection 식과 동일한 식으로
가장 오른쪽부터
3D landmark의 x,y,z 좌표
카메라의 rotation과 translation
카메라의 intrinsic parameter인 K(mono camera인 경우 사용하지 않는다)
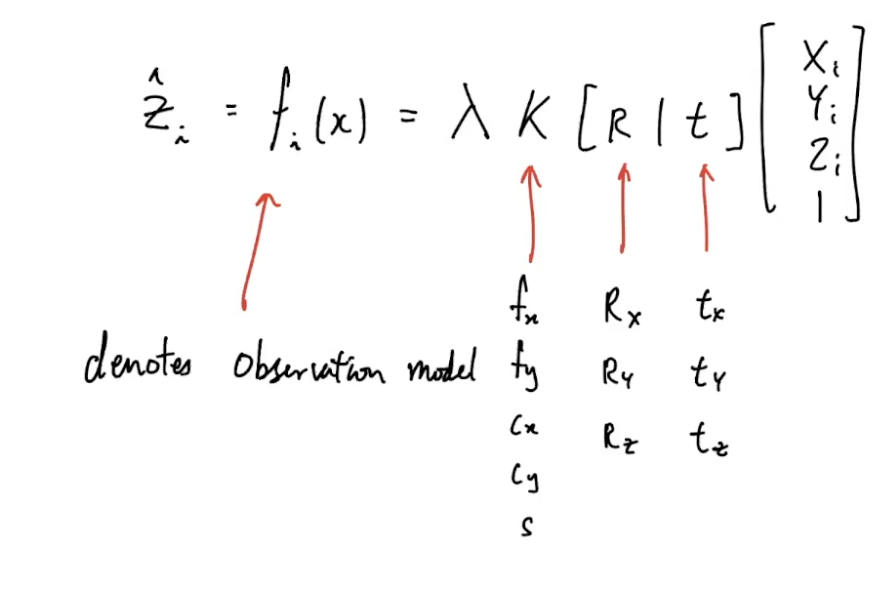
state 벡터로 표현했을 때
landmark는 x,y,z
camera에 대한 state는 T(), R(), scale과 Intrinsic parameter
SLAM state vector는 Xcamera, landmark마다의 x,y,z
로 표현할 수 있다
Bundle Adjustment 최적화 문제는
총 error를 최소화하는 벡터가 가지는 값을 구해야 하는 문제이다
이문제를 풀기 위해 least square optimization를 사용한다
least square 최적화 문제에
노이즈 분포가 가우시안 분포를 가진다고 가정했을 때
Maximum Likelyhood Estimation 문제로 변한다
최적의 값을 구했을 때 통계적으로도 최적화 값인 것이 보장되기 때문이다
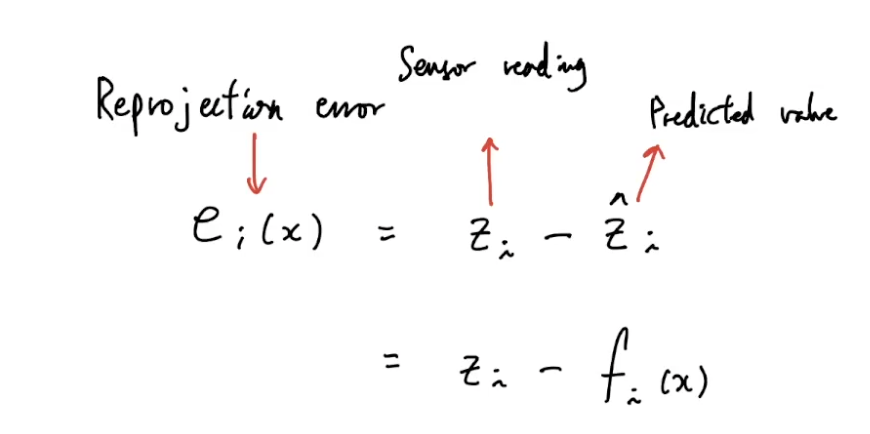
least square 최적화에 가우시안 노이즈 분포를 추가했을 때
아래와 같다

위의 식이 E(x)이고
최적의 값이 x*이면
아래와 같다
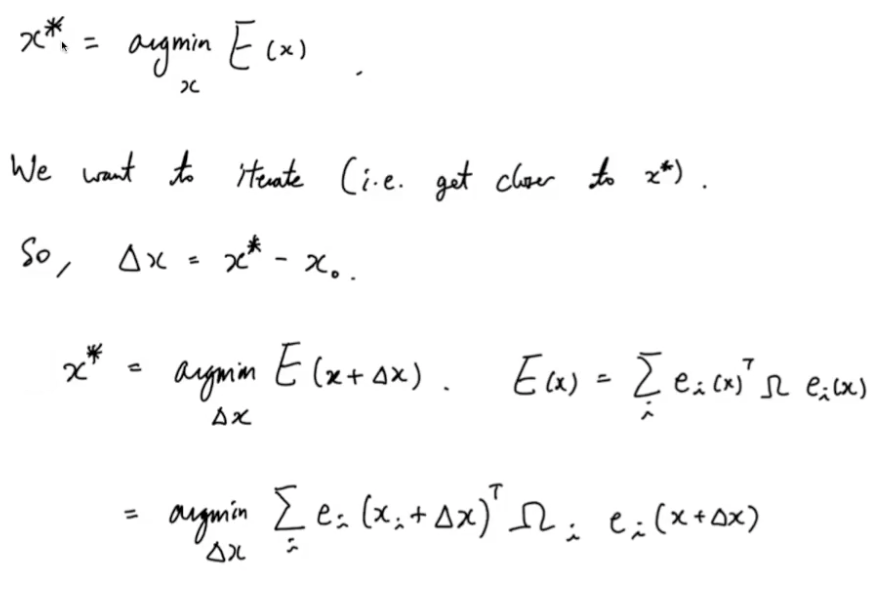
미분을 위해 테일러 expansion을 사용하여
1차 미분에 대한 근사값을 구한다
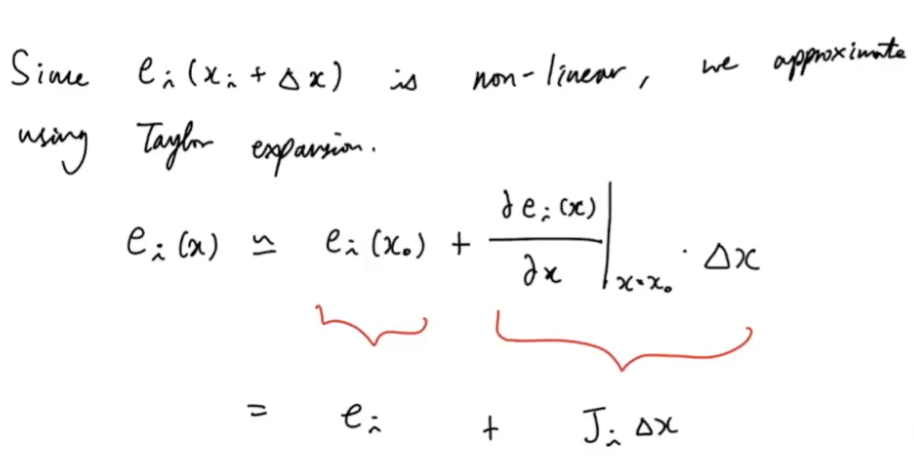
1차 미분 값을 원래 식에 대입한다
정리하면 2차 방정식이 나타난다

2차 방정식의 최소값을 구한다
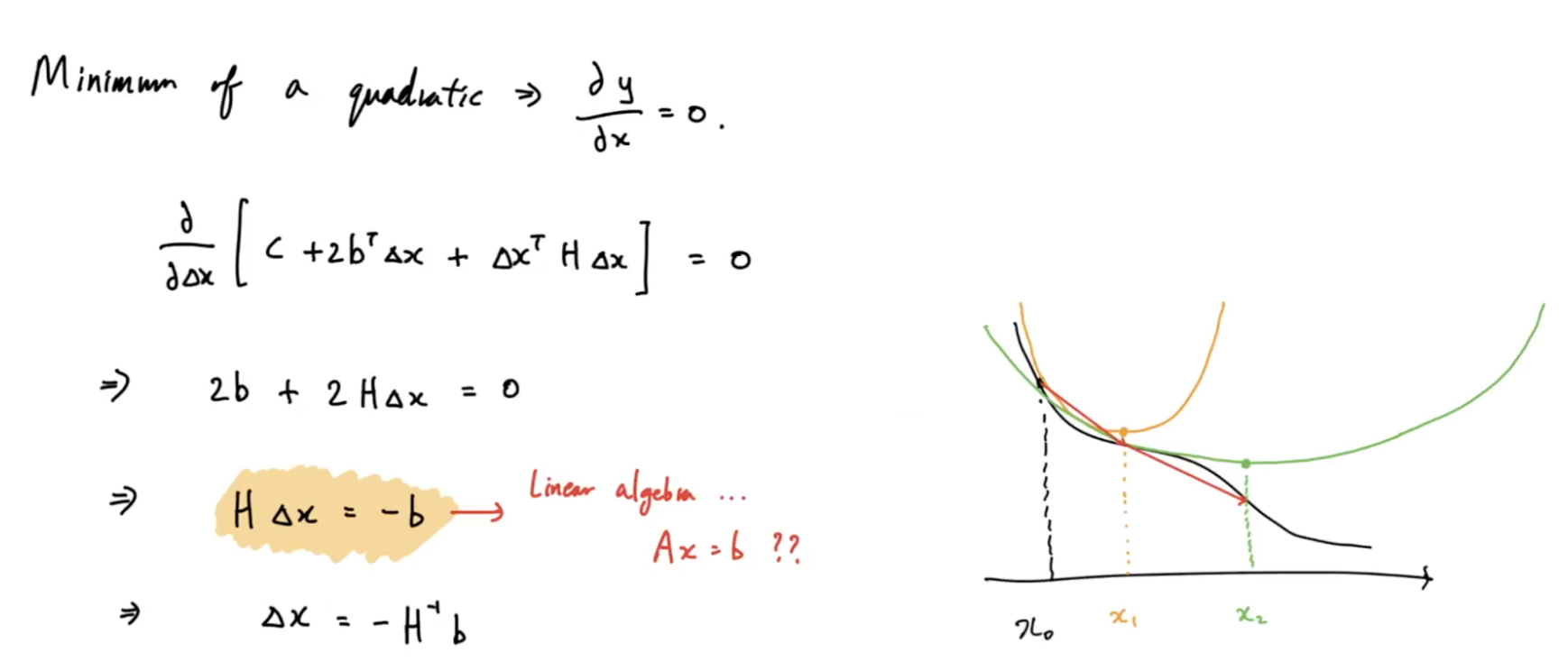
H의 역행렬을 구체적으로 구하기 어렵다

매트릭스 H의 특성을 활용하기 위해
자코비안 행렬에 0이 많은 것을 활용한다
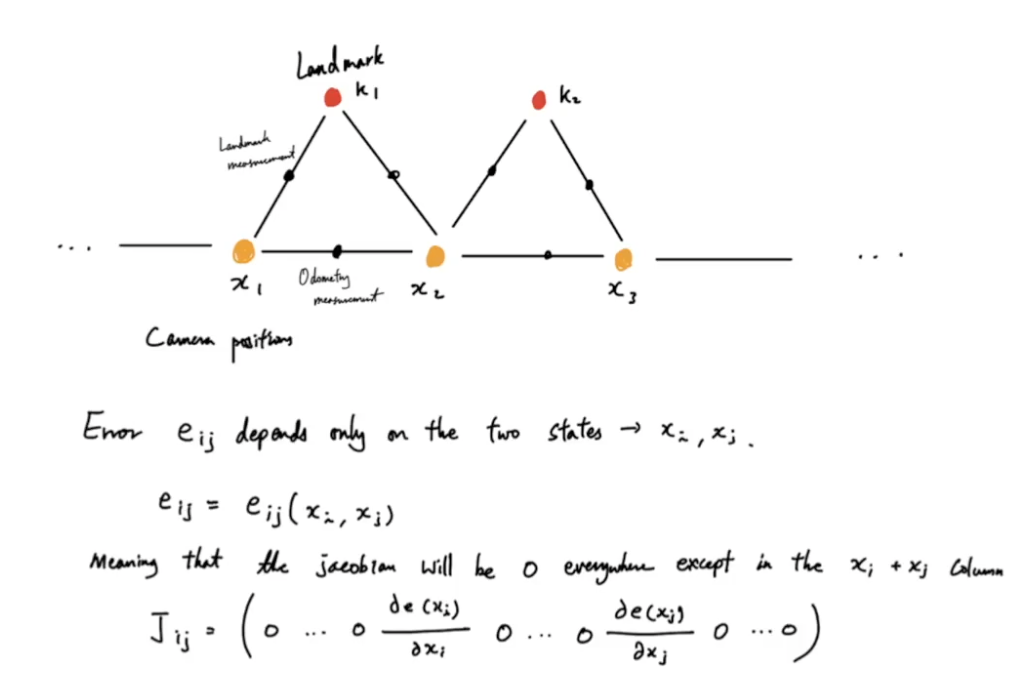
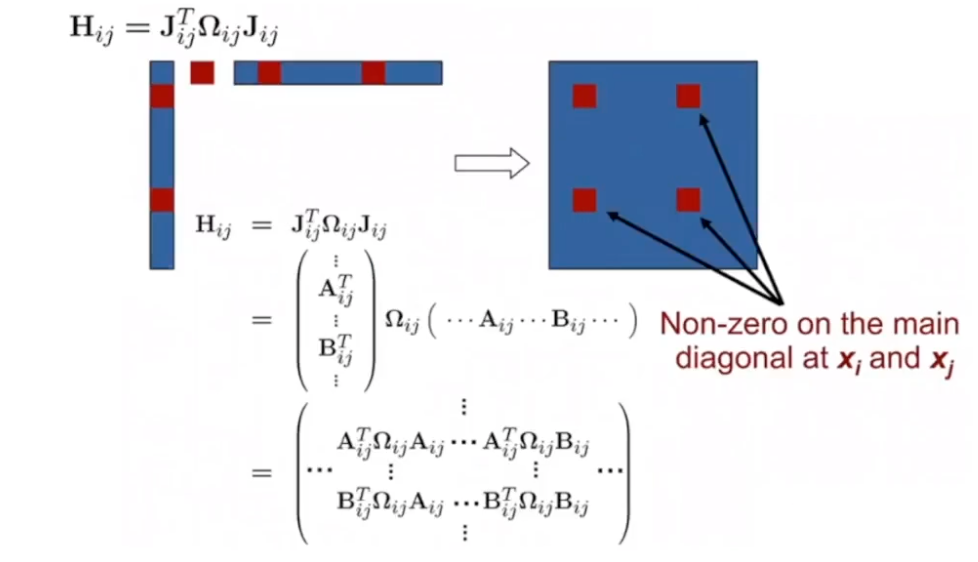
b 행렬 또한 0이 많다

H 행렬도 많이 비어있다
sparse한 행렬 b를 다 더해서 하나의 dense한 행렬로 만들어지고
행렬 h는 더욱 sparse 해진다
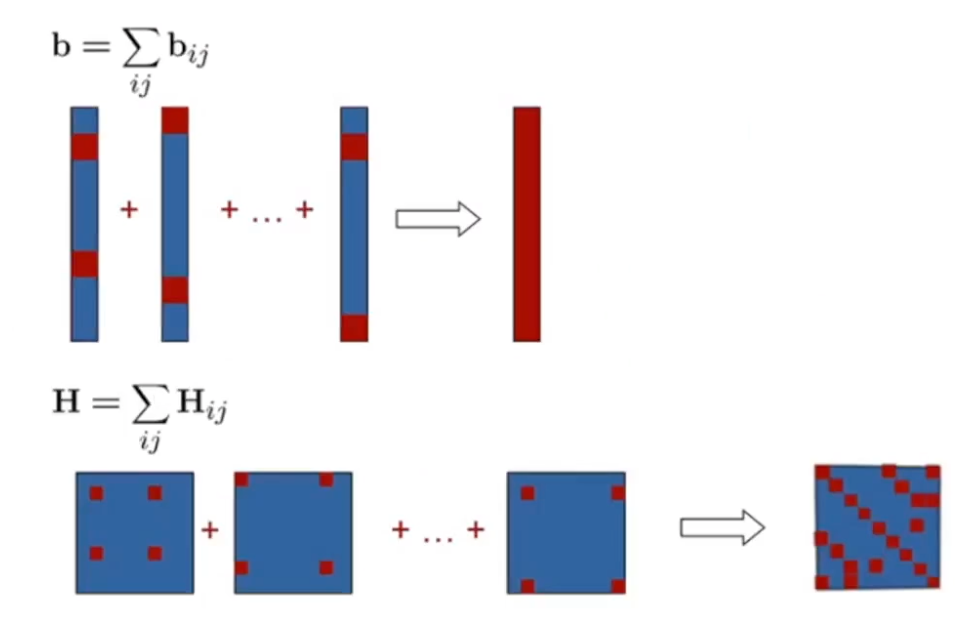
아래 과정을 반복하여
행렬 h를 더욱 빠르게 구한다
sparse 하지만 크기 자체는 크다는 단점이 있다

Schur Complement
Derivation
B에는 카메라 pose에 대한 정보
camera pose는 로봇이 이동할 때마다 생기고
파라미터 수가 많다
새로운 방식으로 적어서
S는 3D 구조에 대한 행렬
SC는 구조와 카메라 와의 correlation, observation에 관한 식이다
C는 카메라에 대한 행렬이다
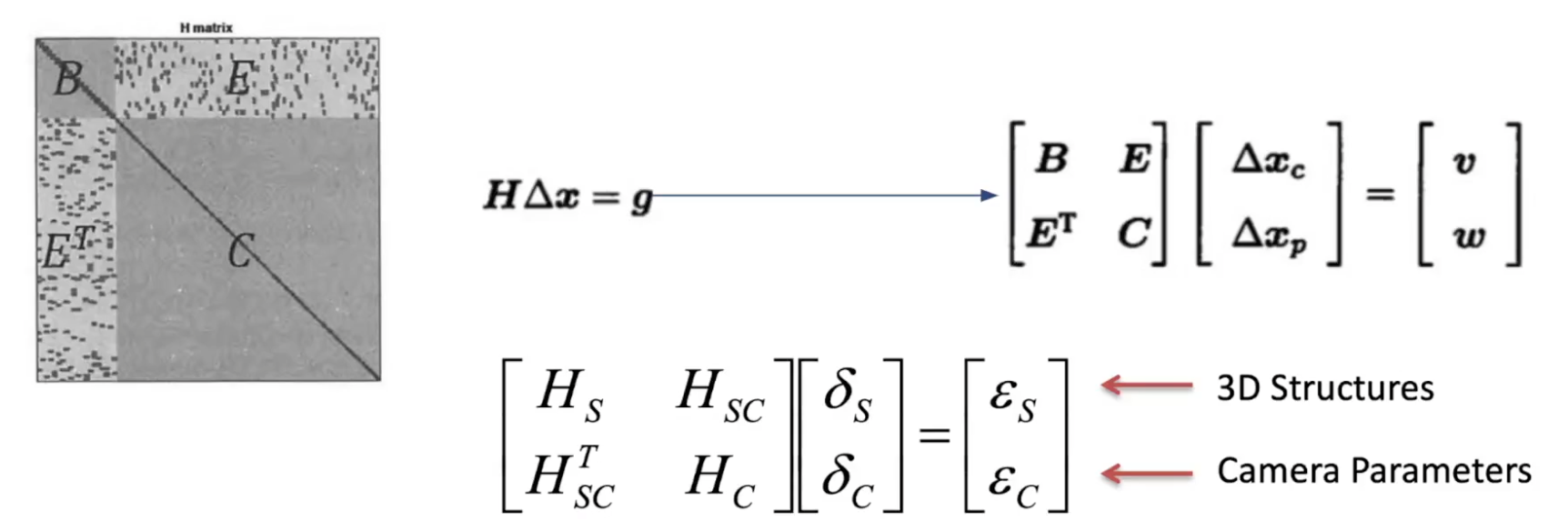
양쪽 변에 다음 행렬을 곱한다
이를 통해 가장 오른 쪽에 델타 없는 행렬을 만든다
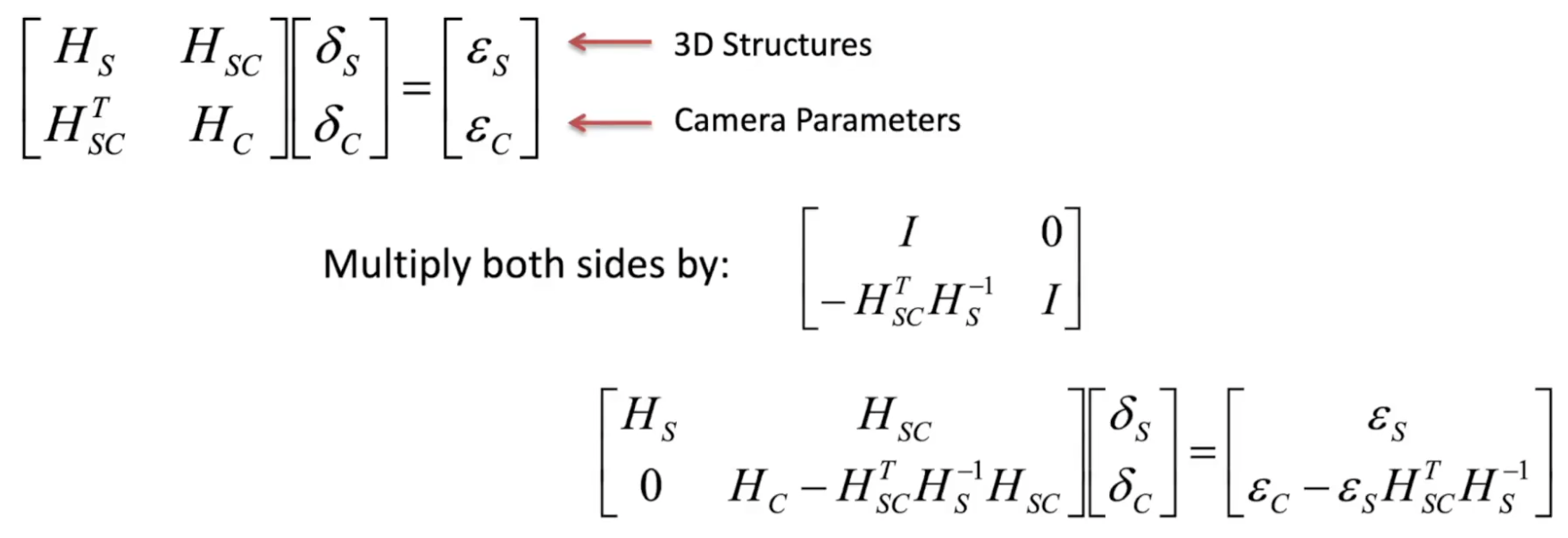
delta C만으로 식을 풀도록 구성을 바꾸면
schur complement를 나타낸다
여기서의 H 역행렬을 구하기는 쉬우므로
큰 행렬 하나로 나타내도록 한다
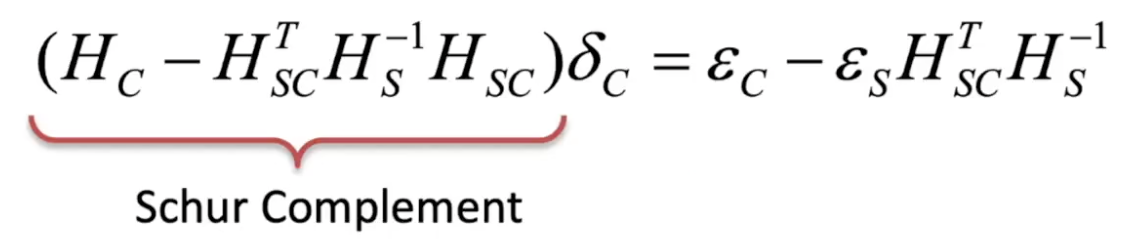
하나의 행렬로 만든 후
역행렬을 구하기 쉬운 형렬로 분해한다
보통 LU decomposition이나 Cholesky decomposition을 사용한다
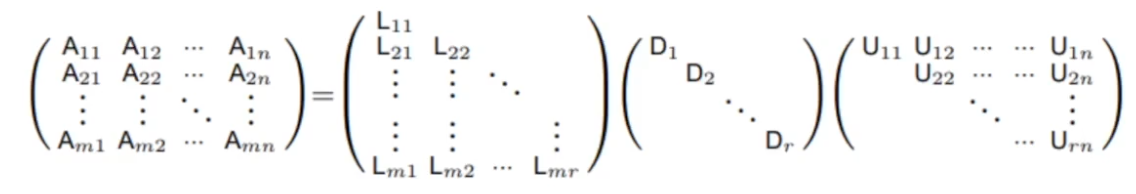
식을 넣어 delta S를 구한다
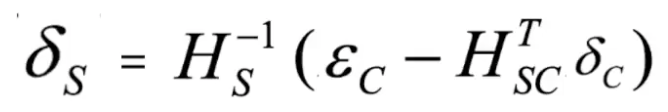
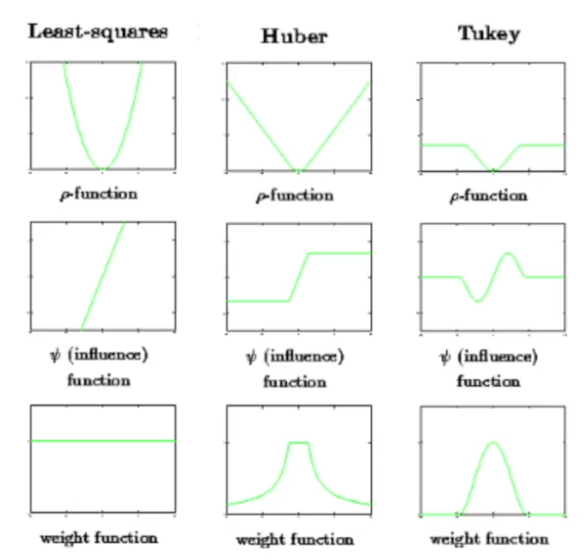
Outlier Rejection
M-estimator
least square non-linear 최적화를 할 때 조심해야 하는 점으로
outliar에 취약하다
데이터의 정상 범주에서 먼 데이터를 제거하여
최적의 값을 구한다
Nonlinear Optimization Libraries
Open Sourced libraries
'SLAM > Visual SLAM' 카테고리의 다른 글
| [VSLAM]최소자승법 (2) | 2023.12.03 |
|---|---|
| [VSLAM]Perspective N Points (2) | 2023.12.03 |
| [VSLAM]Triangulation (1) | 2023.12.02 |
| [VSLAM]RANSAC (1) | 2023.11.28 |
| [VSLAM]Epipolar Geometry (1) | 2023.11.27 |




