Priceless
[ML] 혼자 공부하는 머신러닝+딥러닝 Ch.1 & 2 본문
Ch.1 나의 첫 인공지능
1-1. 인공지능과 머신러닝 딥러닝
인공지능: 사람처럼 학습하고 추론할 수 있는 지능을 가진 컴퓨터 기술
머신러닝: 자동으로 데이터에서 규칙을 학습하는 알고리즘
대표적인 머신러닝 라이브러리로 파이썬을 사용하는 사이킷런(scikit learn)이 있다.
딥러닝: 인공 신경망 기법을 사용한 머신러닝
유명한 머신 러닝 오픈소스: 텐서플로, 파이토치 등
1-2. 코랩과 주피터 노트북
구글 코랩(colab): 브라우저에서 파이썬을 통해 머신러닝 프로그램을 만들 수 있는 서비스
노트북(Notebook): 파이썬을 대화형으로 사용하기 위한 확장자
jupyter 와 colab 등에서 지원한다.
1-3. 마켓과 머신러닝
분류 문제
특정 데이터들을 여러 종류 중 하나로 정하는 것을 분류라고 한다
전체 data source: Fish market | Kaggle
길이가 30cm 이상인 경우 '도미'로 분류하는 식을
아래와 같이 표현한다
if fish_length >= 30:
print("도미")
data source: 도미의 길이, 무게 데이터 (github.com)
도미(bream)의 무게와 길이 등을 특징(feature)이라고 한다
bream_length = [25.4, 26.3, 26.5, 29.0, 29.0, 29.7, 29.7, 30.0, 30.0, 30.7, 31.0, 31.0,
31.5, 32.0, 32.0, 32.0, 33.0, 33.0, 33.5, 33.5, 34.0, 34.0, 34.5, 35.0,
35.0, 35.0, 35.0, 36.0, 36.0, 37.0, 38.5, 38.5, 39.5, 41.0, 41.0]
bream_weight = [242.0, 290.0, 340.0, 363.0, 430.0, 450.0, 500.0, 390.0, 450.0, 500.0, 475.0, 500.0,
500.0, 340.0, 600.0, 600.0, 700.0, 700.0, 610.0, 650.0, 575.0, 685.0, 620.0, 680.0,
700.0, 725.0, 720.0, 714.0, 850.0, 1000.0, 920.0, 955.0, 925.0, 975.0, 950.0]
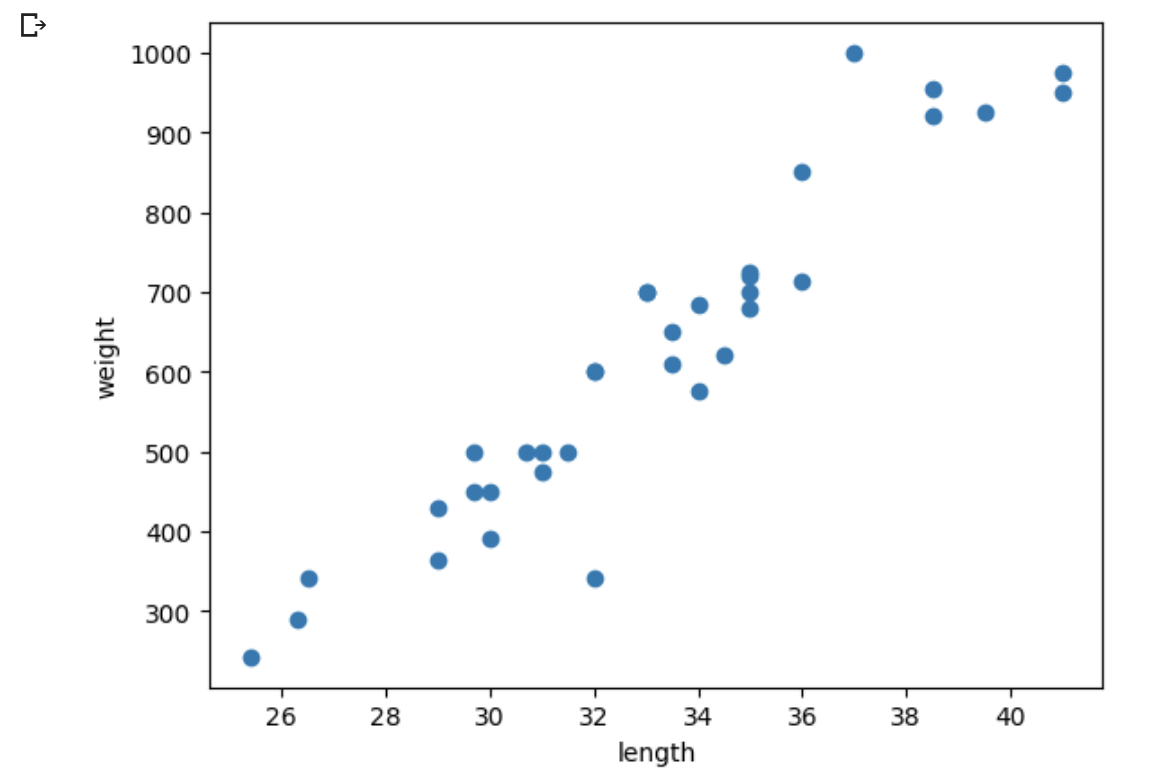
분류를 위한 라이브러리 matplotlib에서 평면도를 위한 pyplot를 사용하여 출력
import matplotlib.pyplot as plt
plt.scatter(bream_length, bream_weight)
plt.xlabel('length')
plt.ylabel('weight')
plt.show()결과
간단한 머신러닝 구현
데이터 설정:
zip() 함수를 통해 두 1차원 데이터를 하나의 2차원 데이터로 생성한다
도미(bream)와 빙어(smelt)의 길이와 무게를 하나의 데이터로 표현한다
smelt_length = [9.8, 10.5, 10.6, 11.0, 11.2, 11.3, 11.8, 11.8, 12.0, 12.2, 12.4, 13.0, 14.3, 15.0]
smelt_weight = [6.7, 7.5, 7.0, 9.7, 9.8, 8.7, 10.0, 9.9, 9.8, 12.2, 13.4, 12.2, 19.7, 19.9]
length = bream_length + smelt_length
weigth = bream_weight + smelt_weight
fish_data = [[l,w] for l, w in zip(length, weigth)]
print(fish_data)
타겟 설정:
도미를 타겟을 설정하여 35개의 도미 데이터는 1, 14개의 빙어 데이터는 0으로 매핑한다
찾으려는 대상을 1로 놓고 그 외를 0으로 설정한다
fish_target = [1]*35 + [0]*14
print(fish_target)k-최근접 이웃 알고리즘
모든 데이터가 있어야 사용 가능하다
predict 메서드를 통해 주변 데이터와 가장 가까운 직선 거리에 어떤 데이터가 있는지 확인한다
기본 값은 (n_neighbors=5)로 주변 5개의 값을 참고한다
k-최근접 이웃 알고리즘을 사용하기 위해
kn을 통해 KNeighborsClassifier 클래스의 객체를 먼저 만든다
객체에 fish_data와 fish_target을 전달하여
fit() 메소드를 통해 도미를 찾기 위한 기준을 학습시킨다(훈련, training)
score() 메소드를 통해 모델의 성능을 평가한다
0~1 의 점수를 통해 나타낸다
아래 같은 경우 타겟과 데이터가 같으므로 1점이다
from sklearn.neighbors import KNeighborsClassifier
kn = KNeighborsClassifier()
kn.fit(fish_data, fish_target)
kn.score(fish_data, fish_target)
>>> 1.0도미와 가까운 데이터인 경우 도미로 정답을 예측한다
kn.predict([[30,600]])
>>> array([1])
가장 가까운 데이터 49개(여기서는 모두)를 사용하기 위해
(n_neighbors=49)를 통해 비교하는 이웃의 개수를 49개로 정한다
도미가 빙어보다 많이 때문에 새로운 모든 데이터를 도미로 추론하기 때문에
이 결과는 35/49 와 같다
kn49 = KNeighborsClassifier(n_neighbors=49)
kn49.fit(fish_data, fish_target)
kn49.score(fish_data, fish_target)
>>> 0.7142857142857143
print(35/49)
>>> 0.7142857142857143
Ch.2 데이터 다루기
2-1. 훈련 세트와 테스트 세트
지도 학습과 비지도 학습
훈련 데이터: 입력과 타깃 데이터, 이를 학습하여 정답을 추론한다
특성: 데이터에서 특징이 나타나는 성분
지도 학습: 정답(타깃)이 주어진 학습으로, 데이터가 무엇인지 구분할 수 있다
비지도 학습: 정답(타킷)이 없으므로 학습으로, 데이터가 어떤 것인지 맞힐 수 없다
훈련 세트와 테스트 세트
테스트 세트: 원래 데이터 중 일부를 떼어 내어 평가에 사용하는 데이터
훈련 세트: 훈련에 사용되는 데이터
테스트 세트와 훈련 세트를 혼용하면 안된다
fish_length = [25.4, 26.3, 26.5, 29.0, 29.0, 29.7, 29.7, 30.0, 30.0, 30.7, 31.0, 31.0,
31.5, 32.0, 32.0, 32.0, 33.0, 33.0, 33.5, 33.5, 34.0, 34.0, 34.5, 35.0,
35.0, 35.0, 35.0, 36.0, 36.0, 37.0, 38.5, 38.5, 39.5, 41.0, 41.0, 9.8,
10.5, 10.6, 11.0, 11.2, 11.3, 11.8, 11.8, 12.0, 12.2, 12.4, 13.0, 14.3, 15.0]
fish_weight = [242.0, 290.0, 340.0, 363.0, 430.0, 450.0, 500.0, 390.0, 450.0, 500.0, 475.0, 500.0,
500.0, 340.0, 600.0, 600.0, 700.0, 700.0, 610.0, 650.0, 575.0, 685.0, 620.0, 680.0,
700.0, 725.0, 720.0, 714.0, 850.0, 1000.0, 920.0, 955.0, 925.0, 975.0, 950.0, 6.7,
7.5, 7.0, 9.7, 9.8, 8.7, 10.0, 9.9, 9.8, 12.2, 13.4, 12.2, 19.7, 19.9]
샘플링 편향
샘플링 편향: 훈련 세트와 테스트 세트에 샘플이 골고루 섞여 있지 않아 샘플링이 한쪽으로 치우친 문제
이 문제를 해결하기 위해 원래 데이터를 잘 섞은 후 훈련 세트와 테스트 세트로 나눠야 한다
2-2. 데이터 전처리
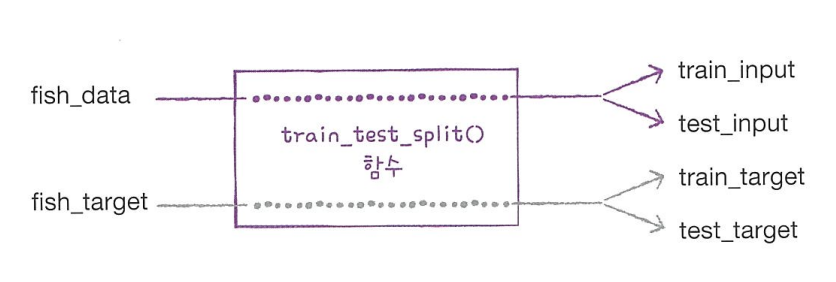
사이킷런으로 훈련 세트와 테스트 세트 나누기
train_test_split()함수를 통해 입력 데이터와 목표 데이터를 훈련 집합과 테스트 집합으로 나눈다
기준 맞추기
데이터 전처리: 샘플 간의 거리의 영향을 위해 일정한 기준으로 맞추는 작업
표준 점수(z 점수): 각 특성 값이 0에서 표준편차의 몇 배만큼 떨어져 있는지 나타내는 점수
특성 값의 크기와 상관 없이 동일한 조건으로 비교할 수 있다
데이터 값에 평균을 빼고 표준 편차를 나누어 구할 수 있다
훈련 세트의 평균과 표준편차를 사용해서 테스트 세트에서도 사용해야 한다
스케일이 다른 특성 처리
길이와 무게 등 특성의 스케일이 다를 때 발생하는 문제를 해결하기 위해 표준점수로 변환
'AI > ML' 카테고리의 다른 글
| [ML]Image Classification과 Pytorch 실습 (1) | 2024.01.07 |
|---|---|
| [ML] 혼자 공부하는 머신러닝+딥러닝 Ch.6 (0) | 2023.08.29 |
| [ML] 혼자 공부하는 머신러닝+딥러닝 Ch.5 (0) | 2023.08.21 |
| [ML] 혼자 공부하는 머신러닝+딥러닝 Ch.4 (0) | 2023.08.15 |
| [ML] 혼자 공부하는 머신러닝+딥러닝 Ch.3 (0) | 2023.08.08 |



